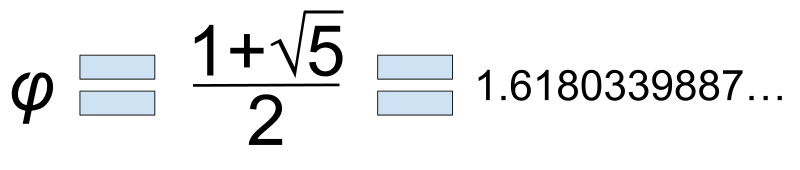
The Golden Ratio
The golden ratio, sometimes also called the divine proportion or golden mean, is a unique number that is predominantly found within mathematics, art and architecture. It has influenced everything from the structure of the pyramids, Beethoven’s music, da Vinci’s Mona Lisa, to the Fibonacci Sequence and urban design.
History
The origins of this equation can be traced back to around 300 BC Greece, where mathematicians such as Euclid and Pythagoras recognised its patterns and proportions and donated it the Greek letter Phi (φ). It was not until later that it gained publicity through the artwork of Leonardo da Vinci and published works by Pacioli in the 16th century.
The Golden Ratio In Nature
It is believed the golden ratio is aesthetically pleasing because it occurs so ubiquitously in the natural world. This can be seen in the ‘golden spirals’ of nautilus shells and animal horns or the ratio of the human body, such as the position of the belly button and facial features. Plants that have adapted the use of the golden ratio grow leaves that hang in such a way as not to shade each other.
Appearance And Influence In Art
It has long been know that designs and paintings that adhere to the golden ratio have harmonious, appealing and balanced compositions. Many famous artistic pieces can be attributed to this rule, such as Leonardo da Vinci’s “The Last Supper” and “The Mona Lisa” and Vincent van Gogh’s “The Starry Night”. Mozart also arranged the number of musical bars in his piano sonatas to this divine ratio, as can be seen in his Piano Sonata No. 1 in C Major.
The Golden Ratio And Mathematics
The golden ratio is a number that is equal to about 1.618. If we divide a line into two parts at the golden ratio (which is just under two thirds), the whole length divided by the longest part would be the same as the long part divided by the short part. The golden ratio is very close to the Fibonacci sequence – a sequence of numbers where each number is the sum of the two proceeding ones. As the sequence increases 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 etc the ratio between the numbers gets closer to the golden ratio.
Modern Applications
Today, the golden ratio is used by many graphic designers and web developers to create visually pleasing layouts, logos and adverts that appeal to audiences. In the field of genetics, scientists have explored the connections between the golden ratio and genetic pattern in DNA strands, while in the field of AI, researchers are investigating the principles of golden ratio inspired algorithms and pattern recognition. It stands as a timeless, universal principle that, with further understanding, will deepen our knowledge of the world around us.
If you have an interest in studying Maths, Oxford Open Learning offers you the chance to do so at several levels, listed below. You can also Contact Us.